基板上の波長λ、電磁波の速度

まず、伝送線路上の基板の電磁波の速度vは下式で表される。

\(\displaystyle\rm v=\frac{λ}{T}=fλ\tag{1}\)

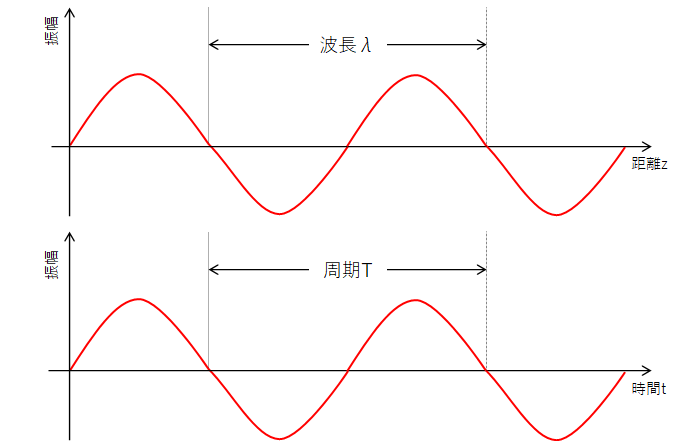
ここで、ｆは周波数、λとTは下図で示す波長と周期を表す。

次に伝送線路の伝搬特性を示す伝搬定数\(\gamma\)は下式で表される。

\(\displaystyle\rm \gamma=α+jβ=\sqrt{(R+jωL)(G+jωC)}\tag{2}\)

ここで、αは減衰定数、βは位相定数と呼ばれ、無損失線路の場合、R=0、G=0となり下式となる。

\(\displaystyle\rm \gamma=α+jβ=jω\sqrt{LC}\tag{3}\)

\(\displaystyle\rm β=ω\sqrt{LC}\tag{4}\)

また、位相定数βは位相の変化の仕方を示す値であり、下式で表される。

\(\displaystyle\rm β=\frac{2π}{λ}\tag{5}\)

上式より波長λは以下となる。

\(\displaystyle\rm λ=\frac{2π}{β}\tag{6}\)

(1)式に(6)式、(4)式を順番に代入し整理すると以下となる。

\(\displaystyle\rm v=fλ=\frac{2πf}{β}=\frac{ω}{β}=\frac{1}{\sqrt{LC}}\tag{7}\)

平行平板伝送線の場合、単位長当たりのC、Lは\(\displaystyle\rm C=\frac{εW}{d}\)、\(\displaystyle\rm L=\frac{μd}{W}\)であるから速度vは以下となる。

\(\displaystyle\rm v=\frac{1}{\sqrt{LC}}=\frac{1}{\sqrt{\frac{μd}{W}\frac{εW}{d}}}=\frac{1}{\sqrt{εμ}}=\frac{c}{\sqrt{ε_rμ_r}}\tag{8}\)

ここで、\(\displaystyle\rm c=\frac{1}{\sqrt{ε_0μ_0}}\)である。

(8)式からわかるように、基板上の電磁波の速度は比誘電率、比透磁率によって変化する。
例えば、ガラスエポキシ基板の場合、比誘電率4.5、比透磁率1であるから速度vは以下となる。

\(\displaystyle\rm v=\frac{c}{\sqrt{4.7}}=\frac{c}{2.17}\tag{9}\)

そして、(1)式から\(\displaystyle\rm λ=\frac{v}{f}\)であるので、基板上の波長λは以下となる。

\(\displaystyle\rm λ=\frac{\frac{c}{2.17}}{f}=\frac{c}{f2.17}=\frac{λ_0}{2.17}\tag{10}\)

上式からわかるとおり、基板上の波長λは速度が遅くなったことにより、真空中の波長λ₀に比べ短くなる。この効果は波長短縮率と呼ばれる。