直流、交流、複素数で表現するいろいろな消費電力の定義
消費電力とひとことで言っても、直流電力、交流電力、瞬時電力、平均電力、複素電力、有効電力、無効電力、皮相電力等様々なものがある。ここではエンジニアが混乱しないように各種消費電力について整理する。
説明は直流電力、交流電力(瞬時電力、平均電力)、複素電力(有効電力、無効電力、皮相電力)の順に記載する。
①直流電力
電力Pは、電圧Vと電流Iの積として定義される。また、オームの法則V=RIを用いて、電流と抵抗での表現、電圧と抵抗での表現も可能である。
\(\displaystyle\rm P=VI=I^2R=\frac{V^2}{R}\)
②交流電力
(1)抵抗
交流電力については、抵抗、インダクタ、キャパシタに分けて説明する。交流の電圧、電流は時間とともに変化する。変化する電圧、電流の瞬時の値を用いて、表現した電力を瞬時電力と呼ぶ。また、瞬時電力を一周期分、積分し周期で割った値を平均電力と呼ぶ。
抵抗Rに電流\(\displaystyle\rm i(t)=I_msin(ωt) \) を印可した場合を考える。
電圧v(t)はオームの法則より以下となる。
\(\displaystyle\rm v(t)=Ri(t)=R I_msin(ωt) \)
よって、瞬時電力pR(t)は以下となる。
\(\displaystyle\rm p_R(t)=v(t)i(t)=Ri(t)^2=R I_m^2sin^2(ωt) \)
さらに、倍角の公式より、瞬時電力pR(t)は以下となる。
\(\displaystyle\rm p_R(t)=R I_m^2\frac{1-cos(2ωt)}{2} \tag{1}\)
(1)式より、瞬時電力は電流、電圧の2倍の周波数で振動していることがわかる。
また、平均電力PRは以下となる。
\(\displaystyle\rm P_R==\frac{1}{T} \int_0^T p_R(t) dt=\frac{1}{T} \int_0^TR I_m^2\frac{1-cos(2ωt)}{2} dt= \frac{ R I_m^2 }{2T} \left[t-\frac{1}{2ω}sin(2ωt)\right]_0^T\)
\(\displaystyle\rm =\frac{ R I_m^2 }{2}=R(\frac{ I_m }{\sqrt{2}} )^2= R I_e ^2 \)
同様に電圧v(t)で平均電力を表すと以下となる。
\(\displaystyle\rm P_R = \frac {1}{R}(\frac{ V_m }{\sqrt{2}} )^2= \frac { V_e ^2}{R} \)
ここで、実効値は \(\displaystyle\rm I_e=\frac{I_m}{\sqrt{2}} \) 、 \(\displaystyle\rm V_e=\frac{V_m}{\sqrt{2}} \) で定義される。
(2)インダクタ
インダクタLに電流\(\displaystyle\rm i(t)=\sqrt{2}I_esin(ωt) \) を印可した場合を考える。
電圧v(t)は以下となる。
\(\displaystyle\rm v(t)=L\frac{di(t)}{dt}= \sqrt{2} LI_eωcos(ωt) \)
瞬時電力pL(t)は以下となる。
\(\displaystyle\rm p_L(t)=v(t)i(t)= L\frac{di(t)}{dt} i(t) =2ωLI_e^2 sin(ωt) cos(ωt)\)
さらに、倍角の公式より、瞬時電力pL(t)は以下となる。
\(\displaystyle\rm p_L(t)=ωLI_e^2 sin(2ωt) \tag{2}\)
平均電力PLは、(2)式からわかるように0となる(sin関数の1周期分の積分値は0となる)。
(3)キャパシタ
キャパシタCに電圧\(\displaystyle\rm v(t)=\sqrt{2}V_esin(ωt) \) を印可した場合を考える。
電流i(t)は以下となる。
\(\displaystyle\rm i(t)=C\frac{dv(t)}{dt}= \sqrt{2} CV_eωcos(ωt) \)
瞬時電力pC(t)は以下となる。
\(\displaystyle\rm p_C(t)=v(t)i(t)= C\frac{dv(t)}{dt}v(t) =2ωCV_e^2 sin(ωt) cos(ωt)\)
さらに、倍角の公式より、瞬時電力pC(t)は以下となる。
\(\displaystyle\rm p_C(t)=ωLV_e^2 sin(2ωt) \tag{3}\)
平均電力PCは、(3)式からわかるように0となる(sin関数の1周期分の積分値は0となる)。
③複素電力
複素電力(complex power)PCとは、電圧 \(\displaystyle\rm V(=V_r+jV_i )\) と電流の複素共役である \(\displaystyle\rm \bar{I} (=I_r-jI_i) \) を乗算したものであり、以下で示される。
\(\displaystyle\rm P_C=V \bar{I} =( V_r+jV_i )( I_r-jI_i )=(V_rI_r+V_iI_i)+j( V_iI_r-V_rI_i )\tag{4}\)
また、電圧を \(\displaystyle\rm V=V\angle{θ_1}=Vcos θ_1+jVsin θ_1 \) 、電流を \(\displaystyle\rm I=I\angle{θ_2} = Icos θ_2+jIsin θ_2 \) で表現した場合はPCは以下となる。
\(\displaystyle\rm P_C=V \bar{I} =( Vcos θ_1+jVsin θ_1 )( Icos θ_2-jIsin θ_2 )\)
\(\displaystyle\rm =(IVcos θ_1 cos θ_2+IVsin θ_1 sin θ_2 )+j( IVsin θ_1 cos θ_2-IVcos θ_1 sin θ_2 ) \)
\(\displaystyle\rm =IVcos( θ_1-θ_2)+jIVsin( θ_1 -θ_2) \)
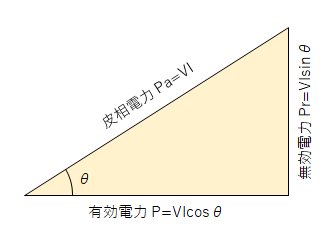
ここで、PCの実部を有効電力(active power) P、虚部を無効電力 (reactive power) Pr、大きさを皮相電力(apparent power) Paと呼ぶ。