負荷端での反射係数Γ、伝送線路上の電圧は2.3項の(3)式、(4.1)式から以下のとおりとなる。
\(\displaystyle\rm Γ=\frac{Z_{L}-Z_{0}}{Z_{L}+Z_{0}}\tag{1}\)
\(\displaystyle\rm V(-l)=V_{+}e^{\gamma l}+V_{-}e^{-\gamma l}=V_{+}(e^{\gamma l}+Γe^{-\gamma l})\tag{2}\)
ここで\(\displaystyle\rm \gamma=α+jβ\)であり、無損失の線路の場合\(\displaystyle\rm \gamma=jβ\)となる。これを上式に代入すると
\(\displaystyle\rm V(-l)=V_{+}(e^{jβl}+Γe^{-jβl})\tag{3}\)
電圧の時間的な変化を考える場合は、(3)式に\(\displaystyle\rm e^{jωt}\)をかければよいから下式となる。
\(\displaystyle\rm V(-l, t)=V_{+}(e^{jβl}+Γe^{-jβl})e^{jωt}=V_{+}(e^{j(ωt+βl)}+Γe^{j(ωt-βl)})\tag{4}\)
① ZL=∞Ω、Z0=50Ωの場合、(1)式、(4)式より負荷端での反射係数Γ、伝送線路上の電圧は以下となる。
\(\displaystyle\rm Γ=\frac{Z_{L}-Z_{0}}{Z_{L}+Z_{0}}=1\)
\(\displaystyle\rm V(-l, t)=V_{+}(e^{j(ωt+βl)}+Γe^{j(ωt-βl)})=V_{+}(e^{j(ωt+βl)}+e^{j(ωt-βl)})\)
そして、ZL=∞Ωの場合の進行波、反射波、電圧のグラフは下図のとおりである。
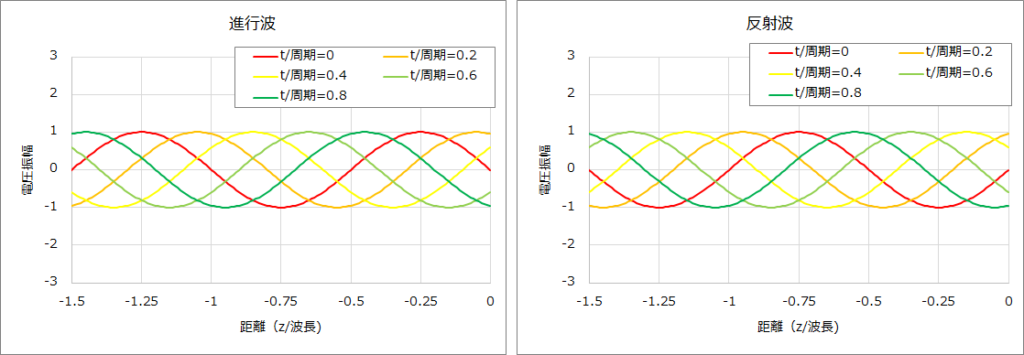
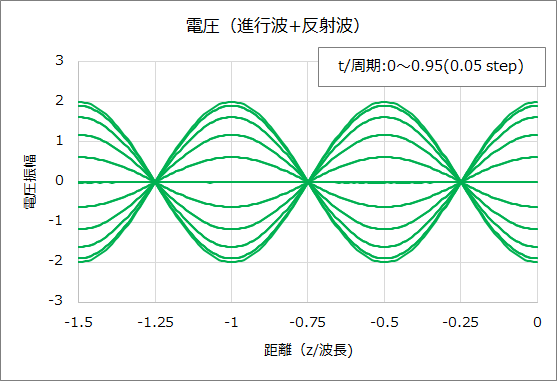
② ZL=0Ω、Z0=50Ωの場合、(1)式、(4)式より負荷端での反射係数Γ、伝送線路上の電圧は以下となる。
\(\displaystyle\rm Γ=\frac{Z_{L}-Z_{0}}{Z_{L}+Z_{0}}=-1\)
\(\displaystyle\rm V(-l, t)=V_{+}(e^{j(ωt+βl)}+Γe^{j(ωt-βl)})=V_{+}(e^{j(ωt+βl)}-e^{j(ωt-βl)})\)
そして、ZL=0Ωの場合の進行波、反射波、電圧のグラフは下図のとおりである。
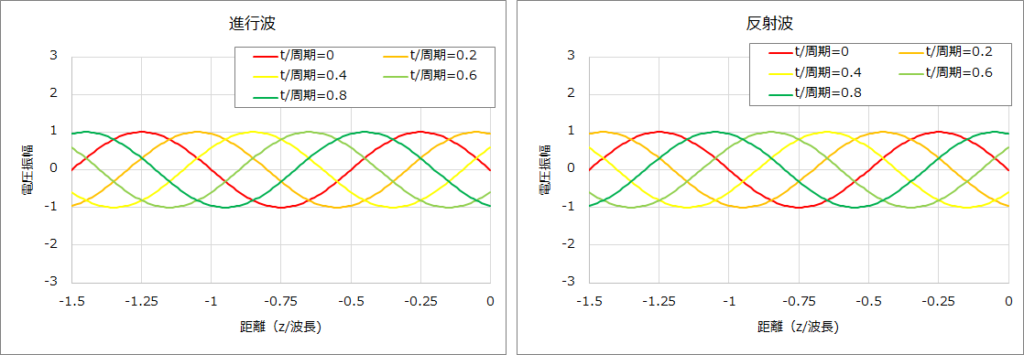
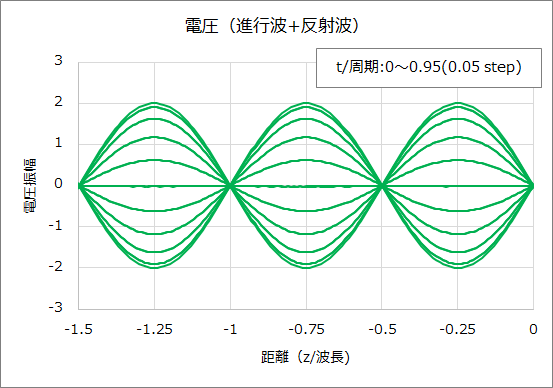
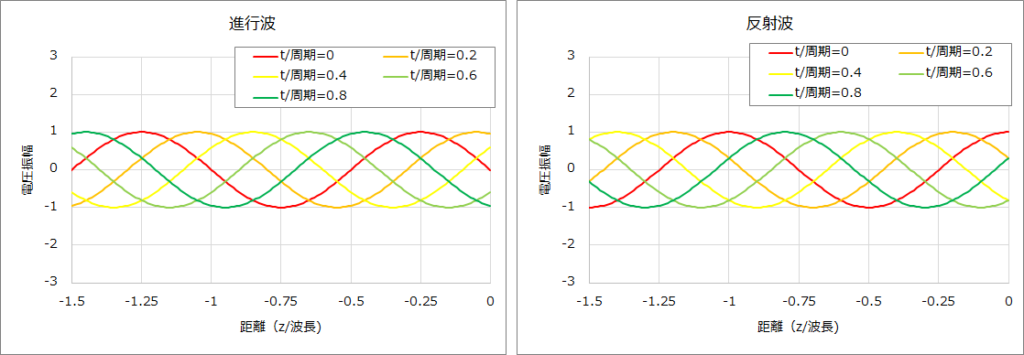
③ ZL=j50Ω、Z0=50Ωの場合、(1)式、(4)式より負荷端での反射係数Γ、伝送線路上の電圧は以下となる。
\(\displaystyle\rm Γ=\frac{Z_{L}-Z_{0}}{Z_{L}+Z_{0}}=j\)
\(\displaystyle\rm V(-l, t)=V_{+}(e^{j(ωt+βl)}+Γe^{j(ωt-βl)})=V_{+}(e^{j(ωt+βl)}+je^{j(ωt-βl)})\)
\(\displaystyle\rm=V_{+}(e^{j(ωt+βl)}+e^{j(ωt-βl+90)})\)
そして、ZL=j50Ωの場合の進行波、反射波、電圧のグラフは下図のとおりである。
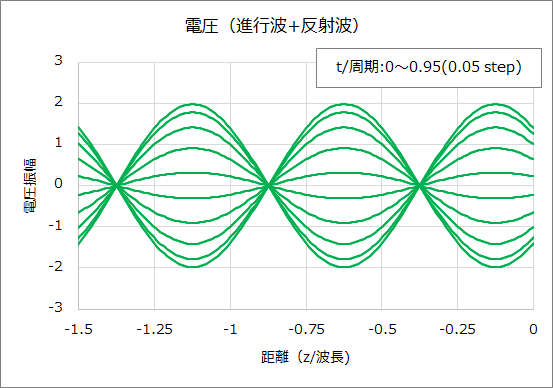
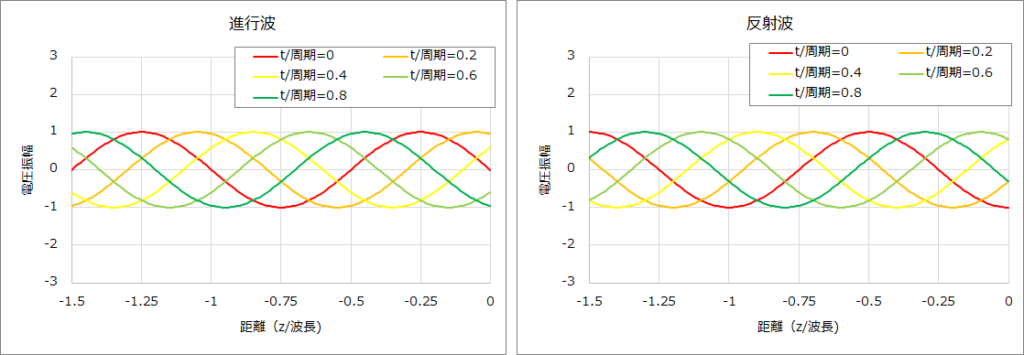
④ ZL=-j50Ω、Z0=50Ωの場合、(1)式、(4)式より負荷端での反射係数Γ、伝送線路上の電圧は以下となる。
\(\displaystyle\rm Γ=\frac{Z_{L}-Z_{0}}{Z_{L}+Z_{0}}=-j\)
\(\displaystyle\rm V(-l, t)=V_{+}(e^{j(ωt+βl)}+Γe^{j(ωt-βl)})=V_{+}(e^{j(ωt+βl)}-je^{j(ωt-βl)})\)
\(\displaystyle\rm=V_{+}(e^{j(ωt+βl)}+e^{j(ωt-βl-90)})\)
そして、ZL=-j50Ωの場合の進行波、反射波、電圧のグラフは下図のとおりである。
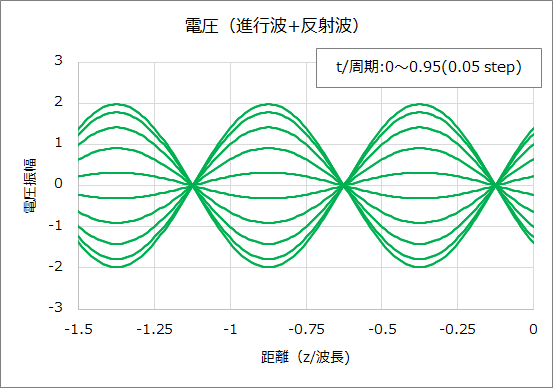
⑤ ZL=150Ω、Z0=50Ωの場合、(1)式、(4)式より負荷端での反射係数Γ、伝送線路上の電圧は以下となる。
\(\displaystyle\rm Γ=\frac{Z_{L}-Z_{0}}{Z_{L}+Z_{0}}=0.5\)
\(\displaystyle\rm V(-l, t)=V_{+}(e^{j(ωt+βl)}+Γe^{j(ωt-βl)})=V_{+}(e^{j(ωt+βl)}+0.5e^{j(ωt-βl)})\)
そして、ZL=150Ωの場合の進行波、反射波、電圧のグラフは下図のとおりである。
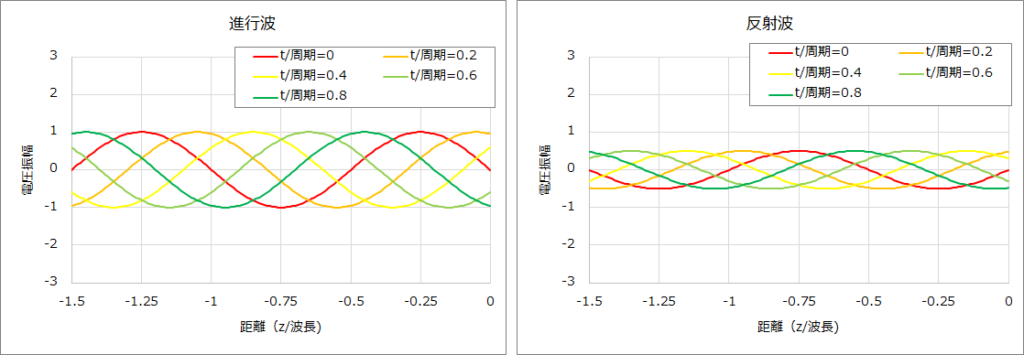
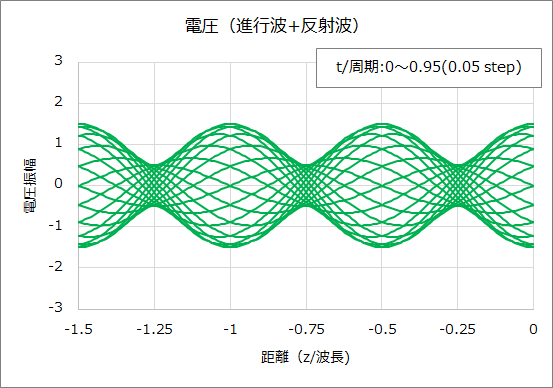
①~⑤に示すとおり、進行波と反射波が合成された電圧波形は、伝送線路の位置によって節と腹が周期的に繰り返す波形となる。
このような電圧波形は波がその場で定在しているように見えることから、定在波と呼ばれ、電圧の場合は電圧定在波と呼ぶ。また、電圧の最大(VMAX))、最小値(VMIN)の比を電圧定在波比(VSWR: Voltage Standing Wave Ratio)と呼び、下式で定義される。VSWRはマイクロ波回路の反射特性の指標として用いられることが多い。
\(\displaystyle\rm VSWR= \frac{V_{MAX}}{V_{MIN}}=\frac{1+|Γ|}{1-|Γ|}\tag{5}\)
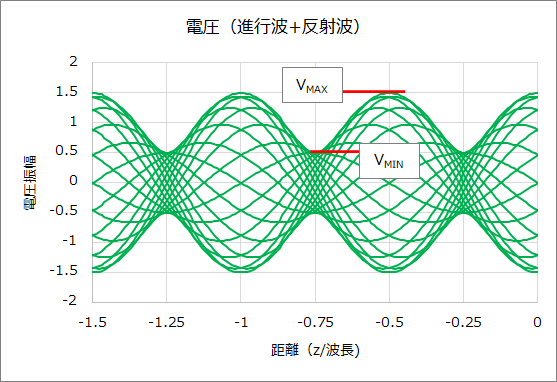
VSWRとは別の反射特性の指標としてはリターンロスがある。リターンロスはマイクロ波回路に入力した電力が、反射して戻ってくる量を表したものであり、下式で定義される。
\(\displaystyle\rm R・L=-20log|Γ|\tag{6}\)
また、不整合による反射の影響によって、損失する電力量はミスマッチロス(M・L)として、下式で表される。
\(\displaystyle\rm M・L=-10log(1-|Γ|^2)\tag{7}\)
