マイクロ波回路では回路の特性を表す際にSマトリクスを使用するのが便利である。ここでは、Sマトリクスの他、2端子対回路を表現する代表的なマトリクスを紹介する。マトリクスを使うことで、回路を入出力の関係だけで表すことができ、扱いが容易になる。
1.Zマトリクス
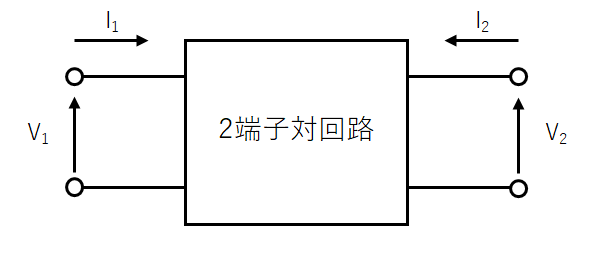
Zマトリクスはインピーダンスで回路の特性を表したものである。下図で定義されたV1、V2とI1、I2の関係を表す。
\(\left[\begin{array}{c}V_{1} \\V_{2}\end{array}\right]=\left[\begin{array}{cc}Z_{11} &Z_{12}\\Z_{21} &Z_{22}\end{array}\right]\left[\begin{array}{c}I_{1} \\I_{2}\end{array}\right]\)
上記、Z11、Z12、Z21、Z22をZパラメータと呼ぶ。
行列式を展開すると以下のとおりとなる。
\(V_{1}=Z_{11}・I_{1}+Z_{12}・I_{2}\)
\(V_{2}=Z_{21}・I_{1}+Z_{22}・I_{2}\)
Zパラメータは入力側ポートを開放(I1=0)させることでZ12、Z22、出力側ポートを開放(I2=0)させることでZ11、Z21が求められる。
2.Yマトリクス
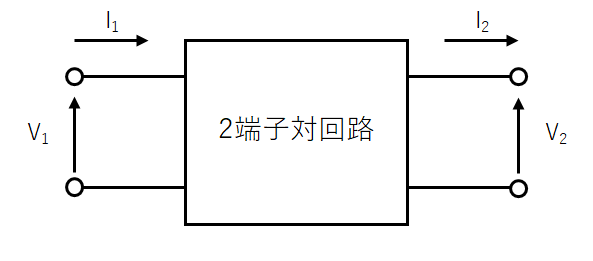
Yマトリクスはアドミタンスで回路の特性を表したものである。下図で定義されたI1、I2とV1、V2の関係を表す。
\(\left[\begin{array}{c}I_{1} \\I_{2}\end{array}\right]=\left[\begin{array}{cc}Y_{11} &Y_{12}\\Y_{21} &Y_{22}\end{array}\right]\left[\begin{array}{c}V_{1} \\V_{2}\end{array}\right]\)
上記、Y11、Y12、Y21、Y22をYパラメータと呼ぶ。
行列式を展開すると以下のとおりとなる。
\(I_{1}=Y_{11}・V_{1}+Y_{12}・V_{2}\)
\(I_{2}=Y_{21}・V_{1}+Y_{22}・V_{2}\)
Yパラメータは入力側ポートを短絡(V1=0)させることでY12、Y22、出力側ポートを短絡(V2=0)させることでY11、Y21が求められる。

3.Fマトリクス(ABCDマトリクス)
Fマトリクスは下図で定義されたV1、I1とV2、I2の関係を表したものである。Zマトリクス、YマトリクスとI2の向きの定義が異なるので注意が必要である。Fマトリクスは縦続接続された回路の計算を行う際に有効なマトリクスである。
\(\left[\begin{array}{c}V_{1} \\I_{1}\end{array}\right]=\left[\begin{array}{cc}A & B\\C & D\end{array}\right]\left[\begin{array}{c}V_{2} \\I_{2}\end{array}\right]\)
上記、A、B、C、DをFパラメータ(ABCDパラメータ)と呼ぶ。
行列式を展開すると以下のとおりとなる。
\(I_{1}=A・I_{2}+B・V_{2}\)
\(V_{1}=C・I_{2}+D・V_{2}\)
Fパラメータは出力側ポートを開放(I2=0)させることでB、D、出力側ポートを短絡(V2=0)させることでA、Cが求められる。
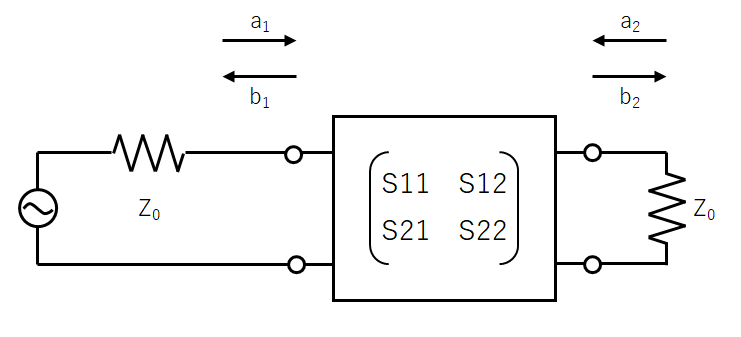
4.Sマトリクス
マイクロ波帯では、測定に用いるプローブや周囲の環境の影響を受け、電圧や電流を正確に取得することができない。このため、電力によって回路を表すSパラメータ(Scattering Parameter)が用いられる。
Sパラメータは前進波(入射波)anと後進波(反射波)bnの関係を表したものである。
anとbnは以下で定義される。
\(\displaystyle a_{n}=\frac{V_{n}^{+}}{\sqrt{Z_{0}}}=I_{n}^{+}\sqrt{Z_{0}}\)
\(\displaystyle b_{n}=\frac{V_{n}^{-}}{\sqrt{Z_{0}}}=I_{n}^{-}\sqrt{Z_{0}}\)
anとbnは2乗すると、前進波、後進波の電力を表すパラメータである。
\(\displaystyle (a_{n})^{2}=\frac{(V_{n}^{+})^{2}}{Z_{0}}=(I_{n}^{+})^{2}{Z_{0}}\)
\(\displaystyle (b_{n})^{2}=\frac{(V_{n}^{-})^{2}}{Z_{0}}=(I_{n}^{-})^{2}{Z_{0}}\)
2ポートの場合のSパラメータは以下で表される。
\(\left[\begin{array}{c}b_{1} \\b_{2}\end{array}\right]=\left[\begin{array}{cc}S_{11} & S_{12}\\S_{21} & S_{22}\end{array}\right]\left[\begin{array}{c}a_{1} \\a_{2}\end{array}\right]\)
行列式を展開すると以下のとおりとなる。
\(b_{1}=S_{11}・a_{1}+S_{12}・a_{2}\)
\(b_{2}=S_{21}・a_{1}+S_{22}・a_{2}\)
Sパラメータは出力側ポートを終端(a2=0)することでS11、S21、入力側ポートを終端(a1=0)することでS12、S22が求められる。