2.1節で説明した分布定数線路として考えなければならない場合の伝送線路について説明する。
線路に電流が流れると磁界(磁束)が発生するため、インダクタとなる。また、上側線路と下側線路の導体間に挟まれた構造となっているため、キャパシタとなる。抵抗とコンダクタンスは線路の損失である。このことから、伝送線路の等価回路は下図に示すとおりとなり、インダクタンスL、抵抗R、キャパシタンスC、コンダクタンスGの組合せで表現される。

上図から微少区間(Δz)を切り出して考えると等価回路は下図となる。
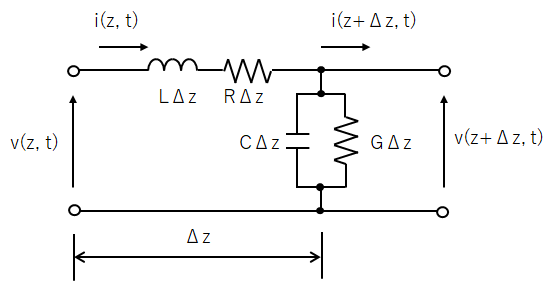
線路の電圧、電流は位置zと時間tの関数である。上図の左端の電圧をv(z, t)、i(z, t)とすると、そこからΔzだけ離れた位置の電圧、電流はv(z+Δz, t)、i(z+Δz, t)となる。上図の回路にキルヒホッフの電圧則、電流則を適用すると以下の式が得られる。
\(\displaystyle\rm v(z, t)-v(z+Δz, t)=RΔz\cdot i(z, t)+LΔz\cdot\frac{\partial i(z, t)}{\partial t}\tag{1.1}\)
\(\displaystyle\rm i(z, t)-i(z+Δz, t)=GΔz\cdot v(z+Δz, t)+CΔz\cdot\frac{\partial v(z+Δz, t)}{\partial t}\tag{1.2}\)
上式の両辺をΔzで割って、Δz→0の極限をとると次の微分方程式が得られる。
\(\displaystyle\rm -\frac{\partial v(z, t)}{\partial z}=L\cdot\frac{\partial i(z, t)}{\partial t}+R\cdot i(z, t)\tag{2.1}\)
\(\displaystyle\rm -\frac{\partial i(z, t)}{\partial z}=C\cdot\frac{\partial v(z, t)}{\partial t}+G\cdot v(z, t)\tag{2.2}\)
電圧v(z, t)、電流i(z, t)を次式で表す。
\(\displaystyle\rm v(z, t)=\sqrt{2} V(z)e^{jωt}\tag{3.1}\)
\(\displaystyle\rm i(z, t)=\sqrt{2} I(z)e^{jωt}\tag{3.2}\)
(3.1)式、(3.2)式を(2.1)式、(2.2)式に代入すると
\(\displaystyle\rm (R+jωL)I(z)=-\frac{d V(z)}{dz}\tag{4.1}\)
\(\displaystyle\rm (G+jωC)V(z)=-\frac{d I(z)}{dz}\tag{4.2}\)
となる。(4.1)式、(4.2)式は伝送線路方程式と呼ばれる。
(4.1)式をzで微分し、(4.2)式を代入してI(z)を消去すると次式が得られる。
\(\displaystyle\rm \frac{d^{2} V(z)}{dz^{2}}=\gamma^{2}V(z)\tag{5.1}\)
(5.1)式は波動方程式と呼ばれる。ここで\(\gamma\)は以下で与えられる。
\(\displaystyle\rm \gamma=\sqrt{(R+jωL)(G+jωC)}=α+jβ\tag{6.1}\)
αは線路単位長あたりの減衰率を与える減衰定数、βは位相変化を与える位相定数である。
(5.1)式の解は次式となる。
\(\displaystyle\rm V(z)=V_{+}e^{-\gamma z}+V_{-}e^{\gamma z}\tag{7.1}\)
(7.1)式を(4.1)式に代入してI(z)を求めると次式となる。
\(\displaystyle\rm I(z)=\sqrt{\frac{G+jωC}{R+jωL}} (V_{+}e^{-\gamma z}-V_{-}e^{\gamma z})=\frac{1}{Z_{0}} (V_{+}e^{-\gamma z}-V_{-}e^{\gamma z})\tag{7.2}\)
ここでZ0は特性インピーダンスと呼ばれ、以下で定義される。
\(\displaystyle\rm Z_{0}=\sqrt{\frac{R+jωL}{G+jωC}}\tag{7.3}\)
(7.1)式、(7.2)式が線路上の電圧、電流を表す重要な式である。
